La geometria del braccio a banana.
Giorni orsono riflettevo riguardo un post pubblicato su uno degli innumerevoli gruppi Facebook ove si confrontano gli appassionati di hifi.
L’autore del post disquisiva sull’acquisto della replica marchiata Bokrand del braccio a banana Ortofon AS-230 e dichiarava l’intenzione di accoppiarlo ad un Thorens TD124.
Da quanto affermava, sembrava che quel braccio avesse delle caratteristiche particolari che lo rendevano preferibile rispetto ad altri o meglio, dalle sue parole mi è sembrato di capire ciò.
Dopo un breve scontro verbale sulla geometria di quel particolare modello e sulla necessità del mio interlocutore di orientarsi verso una replica al posto dell’originale, che avrebbe certamente potuto accaparrarsi a costi nettamente inferiori, peraltro modificata in quanto ridotta a 10″ rispetto agli originari 12″ onde poterla installare sul sopracitato Thorens, la discussione si è interrotta non essendoci da parte dell’interlocutore alcuna propensione al dialogo costruttivo.
Tuttavia mi risulta assai accattivante proseguire la trattazione dell’argomento sulle pagine di Audiosinapsi allo scopo di chiarire alcuni contenuti poco menzionati riguardo la forma di questa tipologia di bracci e soprattutto la geometria risultante.
Va detto che la geometria dei bracci a banana, al pari di qualsiasi braccio imperniato, ed il loro rendimento in termini di contenimento dell’errore e della distorsione radiale, ovviamente dipende anche in questo caso dai tre parametri fondamentali come sappiamo operanti rispetto al piano parallelo al disco, ossia lunghezza effettiva, overhang e angolo offset, anche se quest’ultimo parametro appare celato per via della forma curvilinea della canna.
Ciò nonostante la replica del braccio in questione, sebbene risulti di ottima fattura e perfettamente simile all’originale, come l’originale però soffre di una ulteriore caratteristica geometrica mai analizzata approfonditamente dagli addetti ai lavori, che a mio avviso non dovrebbe farlo preferire rispetto agli altri suoi consimili sempre della medesima forma.
Se mettiamo a confronto i bracci Ortofon AS-230, EMT-997 e Thorens TP-997, ad un occhio non preparato, pertanto non consapevole delle scelte progettuali e del conseguente comportamento geometrico-dinamico, essi appaiono assai simili.
Se dovessimo poi stabilire aprioristicamente, solo per comodità, che i su menzionati bracci abbiano ad esempio la stessa massa effettiva, anche se ciò potrebbe risultare non vero, e pertanto possano essere accoppiati al medesimo fonorivelatore, finirebbe che potrebbero apparire somiglianti e ci si aspetterebbe fossero forieri di prestazioni equivalenti, ma vi posso assicurare non è affatto così!
Uno dei tre sopracitati bracci, suo malgrado, durante l’ascolto risulta affetto di variabilità dell’azimuth, questo è un dato di fatto, anche quando da fermo quest’ultimo valore viene correttamente tarato.
La circostanza della variabilità dell’azimuth tende a verificarsi quando il disco ascoltato risulta minimamente ondulato, non nascondendoci a priori che i dischi che soffrono del su menzionato problema sono tanti, anche se in tanti vantiamo di possederne di perfettamente piani, e magari sono anche quelli che amiamo ascoltare più di frequente.
Vediamo di comprendere per quale motivo l’azimuth risulta così instabile.
Per poter scegliere in maniera oculata e corretta nell’ambito di qualsiasi tipologia di braccio imperniato, compresi quelli a banana, bisognerebbe operare in tal senso.
La scelta andrebbe compiuta preliminarmente su bracci aventi la medesima geometria, in quanto non avrebbe senso svolgere comparazioni tra bracci aventi geometrie diverse.
Successivamente dopo aver ristretto la nostra attenzione su due o tre modelli, aventi le medesime caratteristiche geometriche, da questo momento in poi proseguiremo nella scelta definitiva comparandoli secondo i nostri gusti, ovviamente legati alla capacità musicale dell’oggetto. Ma quali sono queste caratteristiche geometriche?
A questo punto bisogna dire che le caratteristiche geometriche di un braccio a banana comprese quelle di qualsiasi braccio imperniato non sono solo rappresentate dalla lunghezza effettiva, dall’overhang e dall’offset.
In proposito, concentriamo l’attenzione su una ulteriore caratteristica geometrica, sempre interagente rispetto al piano parallelo al disco, ma avente implicazioni dirette riferite al piano perpendicolare al disco passante per il punto di appoggio dello stilo che trovasi ortogonale al piano che contiene il cantilever e l’asse dello stilo.
D’ora in poi questa caratteristica dovrà costituire, al pari delle altre, una scelta fondamentale quando riferita a qualsiasi modello di braccio imperniato.
Per individuare questa ulteriore caratteristica geometrica bisogna indirizzare e soffermare lo sguardo sull’asse di rotazione X, cioè quello passante per il baricentro di ambedue i cuscinetti che permettono al braccio di alzarsi ed abbassarsi rispetto al piano del disco durante l’ascolto.
Quest’asse, come sappiamo, oltre ad essere necessariamente parallelo al predetto piano, dovrà per forza di cose risultare inevitabilmente perpendicolare, non tutti i bracci rispettano questa geometria, rispetto al prolungamento dell’asse longitudinale della shell formando di conseguenza un angolo di 90°.
Nel rispetto di detta geometria quando la shell si alzerà e si abbasserà rispetto al piano del disco il risultato comporterà che il cantilever e di conseguenza l’asse dello stilo rimangano sempre giacenti sul piano perpendicolare a quello del disco.
Questa circostanza inoltre garantisce l’invarianza dell’angolo di azimuth che com’è noto dovrà risultare sempre perpendicolare rispetto al disco.
Osserviamo attentamente la foto A relativa al braccio EMT-997.

Come si può constatare l’asse X passante per i cuscinetti, che permettono alla canna di alzarsi e abbassarsi rispetto al piano del disco, risulta formare rispetto al prolungamento dell’asse longitudinale della shell un angolo β di ampiezza pari a circa 90°.
Bene, questo braccio traslando verticalmente attorno all’asse X, a seguito della rotazione di dischi minimamente ondulati, manterrà l’asse del cantilever e quello dello stilo sempre giacenti sul piano perpendicolare al piano del disco e farà in modo che l’angolo azimuth sia sempre perpendicolare al medesimo piano.

Osserviamo attentamente anche la foto B che questa volta inquadra il braccio Thorens TP-997; anche la geometria di questo braccio è similare all’EMT-997 e determina, pertanto, il medesimo comportamento.
Difatti il segmento X, quello passante per il baricentro dei cuscinetti, forma con l’asse della shell un angolo molto prossimo a 90° che non darà luogo nel caso di dischi ondulati a variazioni repentine dell’azimuth.
A cosa è dovuto un comportamento così rigoroso della shell e di conseguenza del fonorivelatore in ambedue i precedenti bracci?
Notiamo che rispetto all’asse X l’asse corrispondente alla lunghezza effettiva del braccio viene ruotato rispetto all’asse ortogonale all’asse X, facendo perno sul baricentro dello snodo, di un angolo negativo pari al valore offset.
Successivamente, come in qualsiasi braccio, l’angolo offset come sappiamo necessario per ridurre errore e distorsione radiale, questa volta verrà ruotato, facendo perno sullo stilo, di un valore positivo rispetto alla lunghezza effettiva.
Sarà la somma geometrica di questi angoli, ovviamente nulla, che permetterà al braccio di comportarsi in modo da annullare di conseguenza anche qualsiasi variazione dell’azimuth.
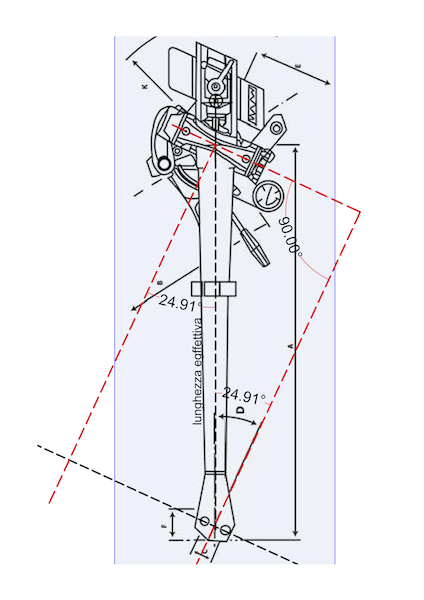
Infine osserviamo la foto C che rappresenta il braccio Ortofon AS-230 tanto osannato dall’autore del post citato in testa al presente articolo.

Notiamo che l’asse X passante per il baricentro dei cuscinetti, quelli che permettono alla canna di alzarsi ed abbassarsi rispetto al disco, risulta in questo caso angolato rispetto al prolungamento dell’asse longitudinale della shell di un angolo β di ampiezza pari a circa 39°, assai minore rispetto al valore corretto dell’angolo β che dovrebbe necessariamente attestarsi, al pari dei casi A e B su 90°, o molto prossimo a questo valore, pena la variazione repentina dell’angolo di azimuth.
E’ proprio la geometria dell’Ortofon che risulta incongruente rispetto ai precedenti modelli, in quanto pur essendo l’asse della lunghezza effettiva ruotato, facendo perno sullo snodo, di un valore angolare pari a quello offset, tuttavia il valore del primo angolo non prende origine da un segmento ortogonale rispetto all’asse X. Il risultato è che l’angolo β è assai inferiore a 90°.
Pertanto, possiamo affermare che via via che l’angolo β diminuisce rispetto al valore ottimale di 90°, l’azimuth, anche se perfettamente tarato, risulta via via sempre più instabile facendo in modo che la shell rolli rispetto al piano del disco di un valore angolare sempre maggiore, il quale risulterà inversamente proporzionale al valore del predetto angolo β.
Pertanto per annullare la variazione azimuth è bene che quest’angolo risulti di 90° o molto prossimo a questo valore.
Come possiamo accorgerci quando abbiamo a che fare con un braccio avente una geometria non proprio corretta.
Semplice; quando il segmento X congiungente il baricentro dei due cuscinetti determinerà con l’asse della canna sul quale scorre in contrappeso un angolo di 90° o assai prossimo, abbiamo a che fare con una geometria scorretta che pertanto genera variazioni repentine dell’azimuth.
Considerando ora i bracci imperniati di forma canonica possiamo fare ulteriori considerazioni:
I successivi disegni rappresentano da sinistra a destra l’arcinoto braccio SME series e lo SME 3009
Valutando la loro geometria dal punto di vista della variazione dell’azimuth; il 3009 risulta perfino migliore dell’Ortofon AS-230, giacché l’angolo di deviazione è pari a circa 48° pertanto più prossimo a 90° rispetto alla deviazione del’Ortofon, che si attesta intorno ai 39°.
Braccio SME SERIES V 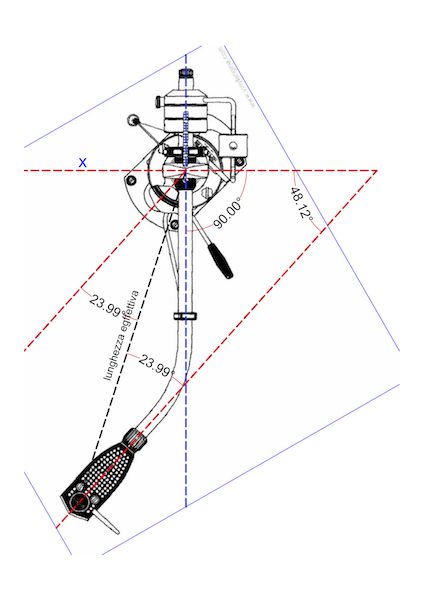
Braccio SME 3009
Infine valutiamo l’aspetto geometrico dello SME series V ove il problema viene risolto, dal comune costruttore, in maniera assai diversa.
Esso rappresenta a mio avviso, ma questo è un parere del tutto personale, il canto del cigno in termini di meticolosa geometria (nei confronti dei tre piani che identificano il comportamento spaziale), combinata a bellezza stilistica e rigorosa interpretazione dal punto di vista musicale.
Come si può osservare l’angolo di deviazione tra l’asse X e il prolungamento dell’asse della shell anche in questo caso è pari a 90°.
Qualcuno sostiene che la variazione dell’azimuth sia minima, ma vorrei anche far notare come le dimensioni dello stilo e del solco siano anch’esse minime, pertanto sarebbe preferibile che durante l’ascolto l’angolo compreso tra l’asse dello stilo e il piano del disco si mantenga rigorosamente costante e pari a 90°, ciò al solo scopo di rilevare correttamente e con la giusta timbrica e dinamica le differenti micro informazioni presenti su ambedue le pareti del solco.
Leggi altro articolo sulla geometria dei bracci
leggi altro articolo di Adriano De Giovanni



